El redondeo a dos cifras significativas arroja una incertidumbre implícita de 1/16 o 6%, tres veces mayor que la del factor menos precisamente conocido. Esta es una buena ilustración de cómo el redondeo puede llevar a la pérdida de información. 1.9E6. El factor "3.1" se especifica a 1 parte en 31, o 3%.. Cifras significativas. Las cifras significativas de una medida son las que aportan alguna información. 1 Representan el uso de una o más escalas de incertidumbre en determinadas aproximaciones. Por ejemplo, se dice que 4,7 tiene dos cifras significativas, mientras que 4,07 tiene tres. Primera: si se necesita expresar una medida con tres.

Cifras significativas YouTube

CIFRAS SIGNIFICATIVAS YouTube

Ejemplos de Cifras Significativas y ejercicios resueltos y propuestos YouTube

Cifras significativas y su manejo135 Clase 2 Número de cifras que son conocidas con algún

La Física & Química en 3º de ESO (El Blog de CHEMA) Expresión de Datos Experimentales Cifras

CIFRAS SIGNIFICATIV AS Las cifras significativas de un

Cifras significativas Noveno Grado Ciencias Naturales YouTube

1.3 Cálculos con Cifras Significativas YouTube

Que Son Las Cifras Significativas

Cómo contar Cifras Significativas YouTube

Unidades y medidas, cifras significativas y redondeo manual y en excel YouTube

Cifras significativas

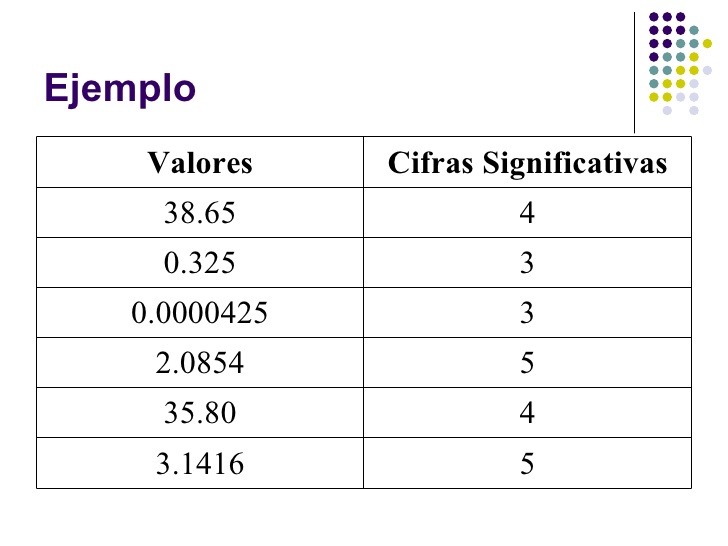
QUIMICA Cifras Significativas

PPT Unidad 1 ( cont ) Cifras significativas PowerPoint Presentation ID6013911

Taller de Cifras Significativas YouTube

Como hacer Redondeo, Cifras Significativas y Decimales significativos de forma fácil YouTube

Reglas de cifras significativas

PPT Unidad 1 ( cont ) Cifras significativas PowerPoint Presentation ID6013911

Cifras significativas

Cifras significativas

Aprende a identificar cifras significativas en un número. En este video se explican las reglas para saber cuando un número es o no una cifra significativa.En.. Los números correctos y el primer número dudoso de una medida son lo que se conoce como cifras significativas. El número de guarismos significativos que se obtienen en una medición, dependen del instrumento que se emplea para realizar la medida. Por ejemplo, si medimos la longitud de un lápiz con una regla cuya menor división es de 1.